数学の問題集の解説が難しすぎて諦めてしまっている受験生諸君へ
こんにちは!
いつもいつもブログでは、ほとんど英語の話しかしない山口です!
いや・・・でも塾生の諸君はご存知の通り、山口数学も教えてるからね!
ブログで英語の話ばっかりなのは、ただ単にPC上で式や図を書くのが本・・・っ当に面倒くさいからなのです。
しかし公立高校入試本番まであと一週間、さすがに面倒くさいなんて言っていられないので、今回は公立高校入試のために、必勝の策を授けたいと思います。
あ・・・、数学が得意な人は読まない方がいいですよ!
今回は、公立高校入試の過去問集の解説を見ても、分かりにくい問題がたまにあるという人向けです。
さて、準備はよろしいか?
それではGO!
こちらは平成25年 B日程の問題です。
塾生から質問をいただきました。どれどれ・・・。
この問題の一番下の(4)番ですね。

見にくいかもしれませんので書いておきます。
【(4)次のページの図で、Oは原点、A、B、C、Dは関数y=ax²(aは定数、a≧0)のグラフ上の点で、線分AD、BCはともにx軸に平行である。
点Aの座標が(-2、8)、点Bのx座標が-1であるとき、次の①②の問に答えなさい。
①aの値を求めなさい。
②点Bを通り、四角形ABCDの面積を2等分する直線の式を求めなさい。】
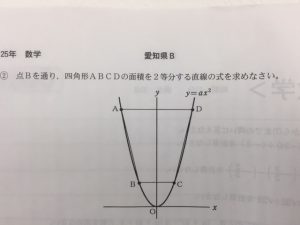
いいね、いいね~!
こういう問題大好きよ!
さて①はとっととA(-2、8)をy=ax²に代入して求めてしまおう。
答 a=2
問題は②ですね。
先に市販の問題集の解説を見てみよう。
これだ!ドーン!

・・・ウソでしょ?
こんな(気付きさえすれば)簡単な問題を、なぜこんなに難しく解説しているんでしょうか?
嫌がらせとしか思えないぞ・・・。
あ、ちなみに数学が得意だ!という生徒諸君は、この解説通りに解いてくださいね。
ここから先は山口流、数学がどうしてもニガテな生徒諸君のための解説になります。
この問題はこういう風に考えれば、90秒で解けます(実際に測りました)。
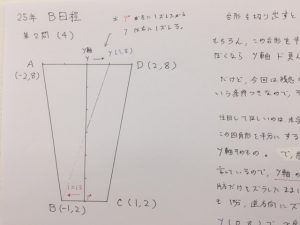
分かりますでしょうか?
まずは、この逆台形の面積を真っ二つにする、一番簡単な直線を考えてみてください。
そう・・・。
誰がどう考えても、縦一直線の『y軸』しかありませんよね?
ただし今回は残念ながら、『点Bを通り・・・』という条件がついているわけです。
そこで多くの受験生は混乱してしまうわけですが、ここでこの問題を解説のように難しく考える必要はまったくありませんよ!
もう一度図を見てください。

点B(-1、2)というのは、y軸そのものを左に『1』ずらした点と言えます。
仮にこの点をy´としましょう。
そう、y´が左にずれてしまったので、どこかで調整をしないと四角形ABCDを半分にする直線式は求められませんね。
ただし全然難しくないですよ!
仮にy´に対して上の点をyとしましょう。
y座標は見ての通り、y(0、8)ですね。
y´が左に1ずれたのだから、今度は上の点yを逆方向に1ずらせば、四角形ABCDを半分にする直線式は求められますね!
y(0、8)が右に1だけずれるのだから、y(1、8)であることはすぐに分かります。
さああとは簡単です!
B(-1、2)とy(1、8)を通る式を求めるだけなので、そのまま『y=ax+b』に代入して連立方程式を解けば、簡単に『y=3x+5』という答えが出ます。


簡単でしょ?
もう一度市販の問題集の解説を見てみましょう。

・・・。
もちろん!どちらでも構わないですよ!
ただ、愛知県の公立高校入試は45分。
第1問の基礎問題9問にかけていい時間が大体7分前後。
第2問の確率や証明問題、関数などなどにかけてよい時間は12分、長くても15分くらい。
第3問以降の『相似な図形』『空間図形』などにかける時間が10~15分。
最後の見直しなども考えると、このレベルの問題には5分もかけられないと肝に銘じてください。
これまでも何度もお伝えしてきましたが、愛知県の公立高校入試問題は、数学についてはそんなに難しくないです。
最後の空間図形は結構厳しい問題もありますが、基本的に基礎問題で7割前後は取れるように作られています。
何が言いたいのかというと、取れる問題は、確実にかつ迅速に解かないと、差がつかないどころか、落としてしまえば逆に致命的なミスになりかねません。
できる限り時間短縮できるように、難しい解法ではなく、簡単かつ確実な解法を選択することをお勧めします。
解説にあるような文字式を使った解き方は、計算の手順が増える分だけミスにもつながりやすいです。
さて、そんなわけで数学で『5点(もちろん100点満点でね)』を取ったことがある、山口ならではの解答テクニック、いかがでしたでしょうか?
数学ニガテなみなさん、ニガテなままでいいじゃないですか。
ありがたいことに、中学数学の解き方は1つじゃないからね!
わざわざ難しくせずに、簡単に簡単に考えましょうね!
そう・・・、そして山口、こういうオリジナルの『時短解答テクニック』を多数まとめておりますが、それは全て塾生のためだけのものですので、ここでは全部は紹介しません!
そうじゃないと、せっかくFIXを選んでくれた塾生諸君に申し訳が立たないってなもんだ。
知りたければぜひぜひ体験授業へカモーン!!!
本日も最後までお読みいただきまして、本当にありがとうございました。
