数学が得意な生徒は読まなくてもOKです(愛知県の公立高校入試 2)
それでは続きになります。
【問題】 ひろ子さんとユリさんは、学校を午後3時30分に出発して図書館に向かった。
ひろ子さんは、学校から図書館までの道のりを歩き、午後4時2分に着いた。
一方、ユリさんはまず学校から自宅までを歩き、自宅から図書館までは自転車で進んだ。
ユリさんの歩いた道のりと自転車で進んだ道のりを合わせると、ひろ子さんの歩いた道のりよりも960m長くなったが、
ユリさんはひろ子さんよりも12分早く図書館に着いた。
学校からユリさんの自宅までの道のりと、ユリさんの自宅から図書館までの道のりは、それぞれ何mであるか。
ただし、2人の歩く速さは毎分60m、ユリさんの自転車の速さは毎分300mである。
写真の通りですが、『距離・速さ・時間』の問題を見つけたらすぐに『きはじ(みはじ)』を書いてください!
なお、『き=距離』『は=速さ』『じ=時間』を表します。

・・・なんかネットで『きはじで問題を解くことは、数学の理解の本質を妨げることになるのでお薦めはしない』みたいな内容を目にしたことがありますが、それは数学を得意な人がやればいいです。
次に『きはじ』と登場人物に合わせて表を作成しましょう。
このとき、問題文に『速さ』についてはすでに書かれてあるので、それは書き込んでしまいます。
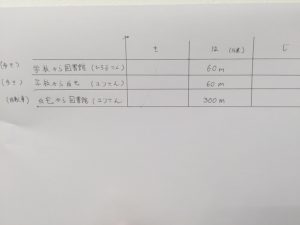
大抵の場合『兄と弟』『A列車とB列車』『行きは歩きで帰りは自転車』といった感じで、登場人物は2人であることがほとんどなのですが、今回は『ひろ子さんの歩き』『ユリさんの歩き』『ユリさんの自転車』と3つの項目が必要になります。
もし分かりにくければ絵を書いてもよいと思います。
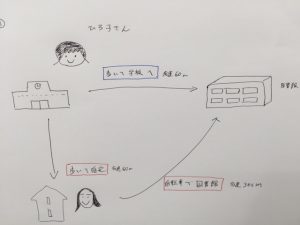
・・・この絵心のなさ。とはいえ、ここで必要なことは情報を整理することです。
ちなみに今回、『きはじ』と『きはじの表』を書くのにかかった時間は1分30秒です。
5分10分かけても分からないくらいなら、1分30秒を犠牲にして確実な答えに辿り着く方がよほど良いかと思います。
さて次です。
これも問題文に『2人とも3時30分に出発してひろ子さんは4時2分に到着、ユリさんはそれよりも12分早く・・・』みたいな記述があるので、これも同じように表に書き込みます。

ここまでを見て分かったと思いますが、現時点で私がやったことは、『きはじの表を書いた』『問題文に書いてあることを表に書き込んだ』だけです。
あ、あと絵を描きましたね(笑)。
さあそしてここからが本番です。
この表より『ひろ子さんは学校から図書館まで、分速60mで歩いて32分かけて到着した』ことが分かっていますので、最初に書いた『きはじ』の距離の部分だけが分からないので『き』を親指で隠します。

するとこの写真の通り、『はやさ × じかん』が残ったので表に書き込まれている情報に基づいて『60×32』からひろ子さんが歩いた距離は『1920m』ということが分かります。これも表に書き込んでしまいましょう。
そしてこの時点で分かっていないのが、『ゆりさんが学校から自宅まで歩いた距離』なのでこれをx、『ゆりさんが自宅から図書館まで自転車で進んだ距離』なのでこれをyとします。
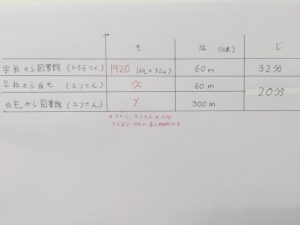
そして問題文より、『ユリさんはひろ子さんよりも960m長く移動している』ことが分かっていますので、これに基づいて次の方程式ができます。
x + y = 1920(ひろ子さんが移動した距離)+960(ユリさんが余分に移動した距離) したがって
【x + y = 2880(m)・・・①】
そして上記の通り表が全てうまっていることを利用して
【x/60 + y/300 = 20(分)・・・②】という式ができます。
もしピンと来なければ、さきほどと同じように『きはじ』の『じ』を隠して『速さ/距離』から時間を求める方程式を立ててください。

あとはこの連立方程式を解いて、x=780(m) y=2100(m)という答えに辿り着きます。
いかがでしたでしょうか?
この問題は公立高校入試レベルではいわゆる難問の部類に入りますが、これくらいなら『数学的ひらめき』などはまったく必要ないことが分かっていただけたかと思います。
①きはじと表を書く
②問題文の情報を全て表に書き込む
③欠けているところに文字を書き込み、方程式をたてる。
ただこれだけです。
以前にも申し上げましたが、愛知県の公立高校入試問題は、その子に合わせてきちんとした計画さえ立ててその通りに進めたなら、どんなに数学がニガテなお子さまでも『絶対に7割以上取れる』ように作られています。
『相似な図形』や『空間図形』の難問を捨てても絶対に7割以上取れます。
しかしながら逆に言えば、それ以外はすべて正解する必要があります。
数学がニガテなみなさん、数学がニガテな私とぜひ一度話してみましょう。
追伸:なお、私以外の先生は学生講師も含めてみな数学は得意です。
